超幾何分布を perl で計算

September 15, 2006

用意するもの

• Mac OS X 10.4.7
• perl 5.8.6
• このスクリプト
  ダウンロード後、拡張子を perl から pl に変えたほうが幸せな人もいるかもしれない。

やってみよう

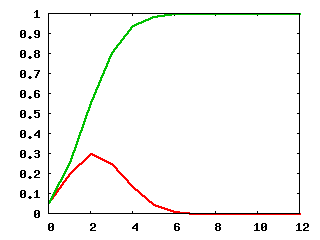
100個のボールのうち赤いものが20個あって、 100個の中からランダムに12個取り出した時に、 12個のうち赤いものがx個になる確率を計算する。 xが0から12までを自動的に計算する。太字のところを入力する。 出力の１カラム目がx、２カラム目が赤いボールがx個になる確率、 ３カラム目が確率を上から足していった値である。ここで、 色以外の属性から赤いボールをできるだけ集めるような クラスタリングの手法を考えるとき、その優劣を定量的に表すには p value を使うのが一般的である。ここでは、クラスタリングの結果赤いボールが x 個拾い出せたとするとき、１から x に対応する第３カラム目の値を引けば p value になる。 12個取り出したときに赤いボールがない確率は約26％、５個入ってる確率は 0.1 % である。あるクラスタリングの手法で赤いボールが３個拾い出せたとき、 その p value は 0.0275 で、かなり良いと判断できる。 参考文献：Z. Tavazoie, Nature Genetics (1999)

• perl ./hypergeometric.pl
• 100 20 12

• 0       0.260750268922344       0.260750268922344
  1       0.396076357856762       0.656826626779105
  2       0.245072246423849       0.901898873202954
  3       0.080682221044889       0.982581094247843
  4       0.0154968900177675      0.998077984265611
  5       0.00179241137554915     0.99987039564116
  6       0.000124473012190912    0.999994868653351
  7       5.02076015559966e-06    0.999999889413506
  8       1.0946424757848e-07     0.999999998877754
  9       1.1184086598057e-09     0.999999999996163
  10      3.81275679479228e-12    0.999999999999975

• (ctrl-D)

スクリプトの中身

超幾何分布の計算には、nCr(組み合わせ)の計算がたくさん出てくる。 母集団の要素数が多くなると階乗がオーバーフローで計算できなくなる。 ので、ガンマ関数の対数を使って計算する。 参考文献：奥村晴彦著、Ｃ言語による最新アルゴリズム事典、技術評論社

while (<>) {
    ($N, $p, $x) = split;
    $s = 0;
    for ($i = 0; $i <= $x; $i++) {
        if ($i > $p) { last; }
        @x = (0, $p+1, $i+1, $N-$p+1, $x-$i+1, $N+1, $x+1);
        $e = &loggamma($x[1]) - &loggamma($x[2]) - &loggamma($x[1]-$x[2]+1)
           + &loggamma($x[3]) - &loggamma($x[4]) - &loggamma($x[3]-$x[4]+1)
           - &loggamma($x[5]) + &loggamma($x[6]) + &loggamma($x[5]-$x[6]+1);
        $e = exp($e);
        $s += $e;
        print "$i\t$e\t$s\n";
    }
}

$PI     = 3.14159265358979324;

sub loggamma
{
    local($x) = @_;
    local($v, $w, @B, $LOG2PI, $N);
    $LOG2PI = 1.83787706640934548;
    $N      = 8;
    @B = (1, -0.5, 0.16666666666666666666, 0, -0.03333333333333333333, 0,
          0.02380952380952380952, 0, -0.03333333333333333333, 0,
          0.07575757575757575757, 0, -0.25311355311355311355, 0,
          1.16666666666666666666, 0, -7.09215686274509803921);

    $v = 1;
    while ($x < $N) { $v *= $x; $x++; }
    $w = 1 / ($x * $x);
    (((((((($B[16]/240)  * $w + ($B[14]/182)) * $w + ($B[12]/121)) * $w
         + ($B[10]/ 90)) * $w + ($B[ 8]/ 56)) * $w + ($B[ 6]/ 30)) * $w
         + ($B[ 4]/ 12)) * $w + ($B[ 2]/  2)) / $x
         + 0.5 * $LOG2PI - log($v) - $x + ($x - 0.5) * log($x);
}